Home

搜索

SearchSearch

椭圆曲线算法

2024年5月20日10分钟阅读

ECC是椭圆曲线加密（Elliptic Curve Cryptography）的缩写，在网络通信以及区块链系统中最常用的加密算法之一。

定义

一条椭圆曲线就是一组被 定义的且满足 的点集。

不同的椭圆曲线对应不同的形状（b=1，a从2到-3）

随着a和b的不同，椭圆曲线也会在平面上呈现出不同的形状，且椭圆曲线始终是关于x轴对称的。需要注意的是，此处还需要一个无穷处的点作为曲线的一部分，用 0 这个符号表示无穷处的点。那么椭圆曲线的表达式为：

群与椭圆曲线上的群论

椭圆曲线算法要用到数学中的群论，那什么是群？简单来说满足下面几个条件（G代表群，a,b是群元素）：

  1. 封闭性：如果a和b被包含于群G中，那么a+b 也一定是G的元素。
  2. 结合律：(a+b)+c=a+(b+c)。
  3. 交换律a+b = b+a.
  4. 存在一个单位元0，使得 a+0 = 0+a = a（单位元：与任意元素运算不改变其值的元素）
  5. 每个数都存在一个相反数。

依此在椭圆曲线上定义群：

  1. 群中的元素就是椭圆曲线上的点。
  2. 单位元就是无穷处的点0.
  3. 相反数P，是关于X轴对称的另一边的点。
  4. 加法规则定义如下：取一条直线上的三点（这条直线和椭圆曲线相交的三点），P, Q, R（皆非零），他们的总和等于0，即P+Q+R=0。

利用几何方法进行椭圆曲线加法

由于椭圆曲线的点集属于一个阿贝尔群，所以我们可以将P+Q+R=0写成 P+Q=−R。这个方程式让我们派生出了一个几何方法去计算两个点P和Q的和：当我们画一条直线通过P，Q，这条线将会和椭圆曲线相交于第三个点R（这就暗示着P，Q，R三点是在一条直线上的）。如果我们取它相反的点，-R， 我们就可以找到P+Q 的结果。

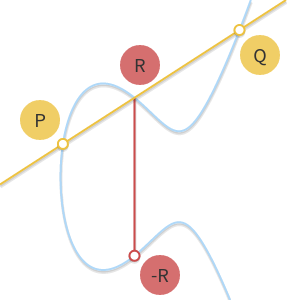
这个几何方法非常有用但是还需要再精炼一下。让我们来回答一下以下几个问题：

  • 如果 P = 0或者 Q = 0 呢？很明显，这样我们是画不出线的，无穷远点0 不在xy平面上。但是我们已经定义了0作为单位元。 P + 0 = P 和 Q + 0 = Q，对于任意的P和Q都适用，单位元的作用就是与任意元素运算不改变其值的元素。
  • 如果P = -Q呢？ 在这种情况下，穿过两点的直线是垂直的，没有相交的第三个点。但是呢，如果P是Q的相反数，然后我们将会从相反数的定义中得到 P+Q=P+(−P)=0。
  • 如果P = Q呢？ 在这种情况下，有无数条线会经过这个点。我们假设一个点 . 当Q’越来越接近P的时候会发生什么？如下图所示。

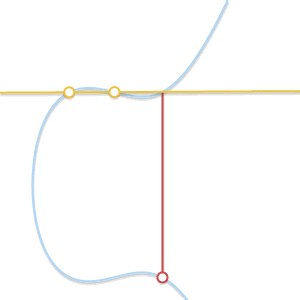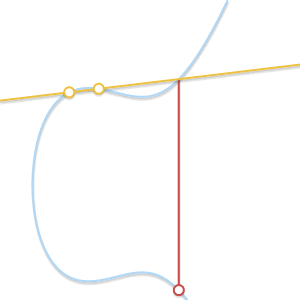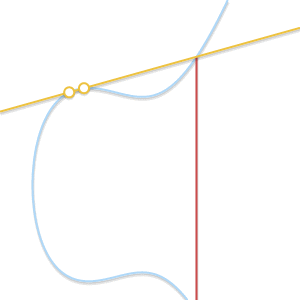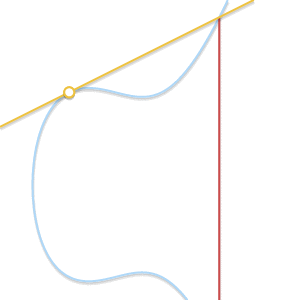
当两点逐渐靠近，穿过两点的直线将会和曲线相切

从上文我们知道，P，Q，R三点在一条线上而且没有先后顺序，这是一般情况。当两个点越来越接近的时候，这条线会成为曲线的一条切线，这条切线与曲线相交的另一点就是R。

鉴于此，当出现切线这种情况时我们可以写成P+P=−R，R是曲线和切线的交点，P是切点。

如果当 P!=Q，但是没有第三点 R 呢？这种情况与上一条非常相似。事实上，这种情况就是一条直线穿过 P 和 Q 与曲线相切。

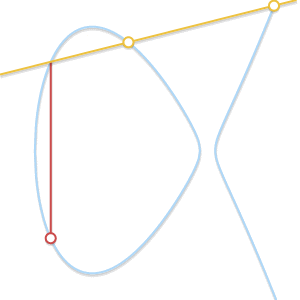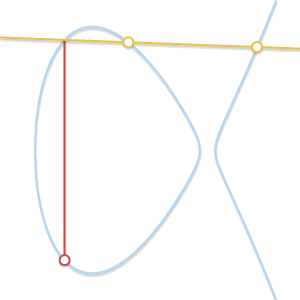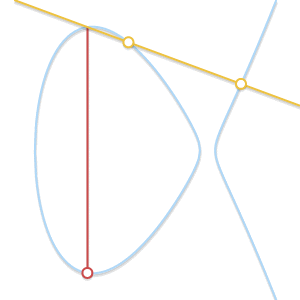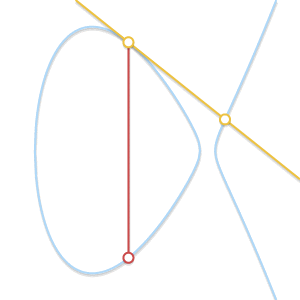
如果直线和曲线仅相交于两点，这意味着直线是曲线的切线。P+Q 的结果显而易见是其中一个点关于X轴的对称点

除上面的几何加法外，还有诸如代数加法、标量积以及对数等方法去求解椭圆曲线，由于不太直观，在此不展开了。

椭圆曲线加密算法

比特币选择的椭圆曲线是名为secp256k1的曲线，secp256k1是一条用于密码学的特定椭圆曲线，它总共包含以下6个参数：

首先是参数，这里的a和b就是椭圆曲线方程中的a和b。也就是这两个参数决定了secp256k1所使用的椭圆曲线方程。secp256k1中它们的值分别是：

a = 0

b = 7

所以方程是 ，在实数域上画出来是这样的：

然后是参数 。因为密码学上使用的椭圆曲线都是在有限域上定义的，对于secp256k1来说，它使用的有限域是 ，也就是它的曲线方程实际上是 。的具体值是：

然后是参数 。  是椭圆曲线上的一个点，称为基点。对于secp256k1，它的具体值是：

G=(55066263022277343669578718895168534326250603453777594175500187360389116729240,32670510020758816978083085130507043184471273380659243275938904335757337482424)

然后是参数 。它是使得的最小正整数。

注意这里的乘法是指定义在曲线上点的乘法，0是指曲线上的零点（无穷远点)。

具体值是：

最后是参数 。一般取 。它是椭圆曲线群的阶跟由生成的子群的阶的比值。是设计secp256k1时使用的参数，在具体实现中使用这个参数主要是出于安全性考虑，忽略它不影响理解。

上面这些就是secp256k1曲线包含的参数及其意义。

下面介绍公钥和私钥是如何生成的。因为这里已经事先选定了secp256k1，所以步骤只有两步：

  1. 用户随机生成一个小于的大整数，这就是私钥。
  2. 然后计算 ，Q即是公钥（公钥是椭圆曲线上的一个点）。

举例

举例： 先生成私钥k k=1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD

K=k * G=(x, y)=(F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A,07CF33DA18BD734C600B96A72BBC4749D5141C90EC8AC328AE52DDFE2E505BDB)

K = (x, y)则为椭圆曲线上一个点。

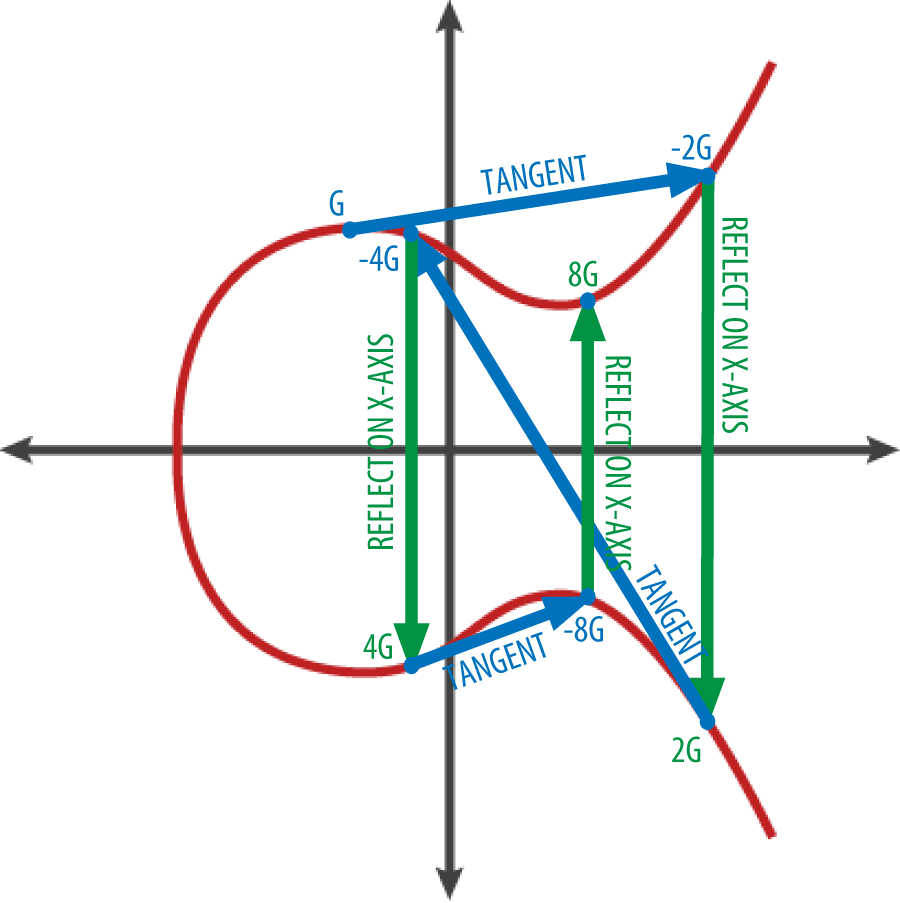
在给定k（私钥）后，如何找到kG（公钥）? 也就是将G相加k次后的点。在椭圆曲线中，点的相加等同于从该点画切线找到与曲线相交的另一 点，然后翻折到x轴。下图显示了在曲线上得到 G、2G、4G 的几何操作，同理可找到kG。

|

参考文章：

关系图谱

反向链接